Here are two problems I used in my calculus 1 class, just after teaching them the definition of the derivative and discussing average and instantaneous rates of change.

1. My car has a digital read out with the average fuel economy.  I used to have a car which also had the instantaneous fuel economy.
   
   What is the difference between these two fuel economies?  Under what circumstances is each more useful?  How can I use the average fuel economy feature to approximate my instantaneous fuel economy?  (Your answer should be  2-5 complete sentences).
2. Read the article at
   http://www.slate.com/blogs/bad_astronomy/2015/09/03/ice_loss_greenland_and_antarctica_lost_5_trillion_tons_since_1992.html .
   You can use this QR code to access it
   
3. Then answer the following questions. Give all answers in complete sentences with units.

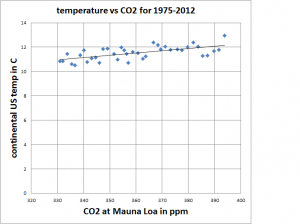
• What is the average rate of change of the mass of Antarctica’s ice?
• What is the average rate of change of the mass of Greenland’s ice?
• Looking at the graphs, do you think it is reasonable to talk about the instantaneous rate of change for these quantities?  Why or why not?

I was so excited about New Horizon’s fly by of Pluto, that I decided to create some math problems about it.  Here they are.  The first one uses the concepts of percent change and volume of a sphere.  The second two use right triangle trigonometry.

1) Answer the question posed in @MathInTheNews ‘s tweet from July 14, 2015:
New Horizons says Pluto’s diameter is 1473mi, 50mi larger than believed. What % does that change its volume estimate?

(Yes, the picture was part of the tweet)

2) Pick two mountains in the large picture of Pluto.  The angle of elevation from the tip of the mountain’s shadow to the tip of the mountain is approximately y/736.5 radians where y is the distance in miles from the base of the mountain to the edge of Pluto in the picture.

a)  What is the height of each of your two mountains?

b) How precise do you think our method is?

c)  Do you think NASA’s claim that there are 11,000 ft high mountains on Pluto is credible?

(Note to other instructors, the estimation of the angle given above is very imprecise, so the students ended up finding mountain heights no more than 7,000 feet high.  In order to improve precision, I printed the following picture out as a 11 by 17 picture).

3) In a July 13, 2015 article for Reuter’s Irene Klotz wrote, “Mysterious Pluto looms large and turns out to be larger than expected as NASA’s New Horizons spacecraft wraps up a nearly decade-long journey, with a close flyby on track for Tuesday, scientists said on Monday.  The nuclear-powered probe was in position to pass dead center of a 60-by-90-mile (97-by-145 km) target zone between the orbits of Pluto and its primary moon, Charon, at 7:49 a.m. EDT (1149 GMT) on Tuesday, said managers at New Horizons mission control center, located at the Johns Hopkins University Applied Physics Laboratory outside of Baltimore. After a journey of 3 billion miles (4.88 billion km), threading that needle is like golfer in New York hitting a hole-in-one in Los Angeles, project manager Glen Fountain told reporters.”

Is this analogy correct?  (You will need to look up some additional numbers and make additional assumptions to answer this question).

Here’s a warm up activity to get students thinking mathematically and thinking about what math is:

One of my friends posted this picture on Facebook.  Use it and whatever other resources you need to answer the following questions.

a) Assuming the first statement is correct, is the second statement correct?

b)  What (if anything) is wrong with this “solution” to homelessness?

c) To what extent was this problem “doing math”?  Were both parts a and b math problems?

This is a problem I work through in my pre-calculus class when we are discussing the meaning of the slope and y-intercept.  It also gives me the opportunity to discuss the perils of extrapolating far outside of the data set.

Consider the following data and the linear model that fits it.

The equation for the linear model is y=0.019x+4.76.  Answer the following questions in complete sentences with units.

1. What are the units for the slope?
2. What does the slope mean in this particular situation?
3. What are the units for the y-intercept?
4. What does the y-intercept mean in this particular situation?

(data from http://www.esrl.noaa.gov/gmd/dv/data/index.php?site=mlo&parameter_name=Carbon%2BDioxide&frequency=Monthly%2BAverages and http://www.ncdc.noaa.gov/cag/ )

The FoxTrot Strip from November 6, 2005 contained a “numerical word search”

You can find the strip here.

There are seven clues which are arithmetic problems, but there is also the derivative of 43981 x , the definite integral of x^3 from 0 to 16, and the sum from k equals 0 to 47 of k squared.    I asked my calculus students to perform all these calculations.

I asked my calculus students to read this xkcd strip from http://xkcd.com/872/

Then I asked them:

a) What is $\lim_{x\rightarrow \infty} (x )$?
b) Explain what might have been weird about the $\lim_{x\rightarrow \infty} (x )$ little pigs.

Randall Munroe drew a lovely comic strip graphing the effects of proximity to a cat on the human intellect:

(You can view it here: http://xkcd.com/231/).

In differential calculus I asked students to describe the graphs using their knowledge of calculus.  Statements about both the first and second derivative are expected.

In Intermediate Algebra here at UDM we study qualitative graphs, so I also asked my Algebra students to describe the graph.  These students have to say things like the intelligence of the human is decreasing, but at an ever faster rate.

One caution with this comic: some students do not know what “inanity” means, so I use this problem on the review sheet rather than the exam.

In this FoxTrot strip Paige has been cramming for her math final and thus is answering all questions in mathematical notation.

http://assets.amuniversal.com/b07d90305e30012ee3bf00163e41dd5b

(Its the May 22, 2005 strip, if the link doesn’t work.)

In precalculus I asked the students:

1) What temperature will it be tomorrow?  Is it going to be hot tomorrow?

(The answer is sin^{-1}(1) =90 degrees, so it will be hot).

2) What does the girl (Paige) want for snack?

(The answer is 3.14159265359…, so she wants pie).

In calculus of sequences and series, you could also ask what the discount was in the fourth panel, which requires computing the sum of an infinite geometric series.

In an algebra class one could ask what time Paige went to bed (\sqrt{121}= 11:00) or What is on TV? (4!=24).

In this FoxTrot strip Jason is “helping” Paige do her homework without even looking in the book.  He claims the answer to question 36 is lim_{x \rightarrow \infty} \frac{x+2}{x-2}.

I asked my students to evaluate this limit, but think this wasn’t a very good use of the comic strip.  If you have a better idea, please comment or email me.

http://assets.amuniversal.com/8e0befc05cee012ee3bd00163e41dd5b

(If the link doesn’t work try going to  http://www.amureprints.com/reprints/sphinx_search , entering the keyword “question” and checking the FoxTrot box.  It was the first hit when I used this search.  The fact that it is from September 13, 2001    may also help you find it.)

Here’s a question I asked my students about limits using http://www.xkcd.com/103/:

1) Using the graph in the comic strip, find

\lim_{speed  \rightarrow c} Rationalization.

2) Write one or two complete sentences explaining what the limit I just had you compute has to do with the text of the comic strip.